Вероятность попадания в заданный интервал нормальной случайной величины

Дисперсия обычной случайной величины.

Дисперсия случайной величины имеется математическое ожидание квадрата соответствующей центрированной случайной величины.

Она характеризует степень разброса значений случайной величины довольно ее математического ожидания, т.е. ширину диапазона значений.

Расчетные формулы:

(6.9)

Дисперсия возможно вычислена через второй начальный момент:

(6.10)

Дисперсия случайной величины характеризует степень рассеивания (разброса) значений случайной величины довольно ее математического ожидания. Дисперсия СВ (как дискретной, так и постоянной) имеется неслучайная (постоянная) величина.

Дисперсия СВ имеет размерность квадрата случайной величины. Для наглядности чёрта рассеивания пользуются величиной, размерность которой сходится с размерностью СВ.

Средним квадратическим отклонением (СКО) СВ X именуется черта

. (6.11)

СКО измеряется в тех же физических единицах, что и СВ, и характеризует ширину диапазона значений СВ.

Свойства дисперсии

Дисперсия постоянной величины с равна нулю.

Подтверждение: по определению дисперсии

При прибавлении к случайной величине Х неслучайной величины с ее дисперсия не изменяется.

D[X+c] = D[X].

Подтверждение: по определению дисперсии

(6.12)

3. При умножении случайной величины Х на неслучайную величину с ее дисперсия умножается на с2.

Подтверждение: по определению дисперсии

. (6.13)

Для среднего квадратичного отклонения это свойство имеет форму:

(6.14)

Вправду, при ½С½1 величина сХ имеет вероятные значения (по полной величине), громадные, чем величина Х. Следовательно, эти значения рассеяны около математического ожидания М[сХ] больше, чем вероятные значения Х около М[X], т.е. . В случае если 0 .

Правило 3s. Для большинства значений случайной величины безотносительная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, либо, иначе говоря фактически все значения СВ находятся в промежутке:

[ m — 3s; m + 3s; ].(6.15)

Возможность попадания в заданный промежуток обычной случайной величины

Как уже было установлено, возможность того, что постоянная случайная величинапримет значение, находящиеся в собствености промежутку, равна определенному интегралу от плотности распределения, забранному в соответствующих пределах:
.
Для нормально распределенной случайной величины соответственно возьмём:
.
Преобразуем последнее выражение, введя новую переменную. Следовательно, показатель степени выражения, стоящего под интегралом преобразуется в:
.
Для замены переменной в определенном интеграле еще нужно заменить пределы и дифференциал интегрирования, предварительно выразив переменную из формулы замены:
;
;
– нижний предел интегрирования;
– верхний предел интегрирования;
(для нахождения пределов интегрирования по новой переменнойв формулу замены переменной были подставленыи –пределы интегрирования по ветхой переменной).
Подставим все в последнюю из формул для нахождения возможности:

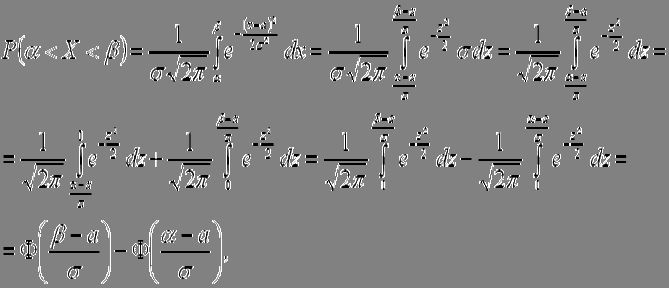
где– функция Лапласа.
Вывод: возможность того, что нормально распределенная случайная величинапримет значение, находящиеся в собствености промежутку, равна:
,
где– математическое ожидание,– среднее квадратическое отклонение данной случайной величины.

23. Распределения «хи-квадрат», Стьюдента и Фишера

Посредством обычного распределения определяются три распределения, каковые на данный момент довольно часто употребляются при статистической обработке данных. В предстоящих разделах книги неоднократно видятся эти распределения.

Распределение Пирсона(хи — квадрат) – распределение случайной величины

где случайные размеры X1, X2,…, Xn свободны и имеют одно и также распределение N(0,1). Наряду с этим число слагаемых, т.е. n, именуется «числом степеней свободы» распределения хи – квадрат.

Распределение хи-квадрат применяют при оценивании дисперсии (посредством доверительного промежутка), при проверке догадок согласия, однородности, независимости, в первую очередь для качественных (категоризованных) переменных, принимающих конечное число значений, и во многих вторых задачах статистического анализа данных [8, 9, 11, 16].

Распределение t Стьюдента – это распределение случайной величины

где случайные размеры U и X свободны, U имеет распределение стандартное обычное распределение N(0,1), а X – распределение хи – квадрат с n степенями свободы. Наряду с этим n именуется «числом степеней свободы» распределения Стьюдента.

Распределение Стьюдента было введено в 1908 г. британским статистиком В. Госсетом, трудившемся на фабрике, производящей пиво. Вероятностно-статистические способы употреблялись для принятия экономических и технических ответов на данной фабрике, исходя из этого ее управление запрещало В. Госсету публиковать научные статьи под своим именем. Таким методом охранялась коммерческая тайна, «ноу-хау» в виде вероятностно-статистических способов, созданных В. Госсетом.

Но он имел возможность публиковаться под псевдонимом «Стьюдент». История Госсета — Стьюдента говорит о том, что еще сто лет назад менеджерам Англии была очевидна громадная экономическая эффективность вероятностно-статистических способов.

На данный момент распределение Стьюдента – одно из самые известных распределений среди применяемых при анализе настоящих данных. Его используют при оценивании математического ожидания, других характеристик и прогнозного значения посредством конфиденциальных промежутков, по проверке догадок о значениях математических ожиданий, коэффициентов регрессионной зависимости, догадок однородности выборок и т.д. [8, 9, 11, 16].

Распределение Фишера – это распределение случайной величины

где случайные размеры Х1 и Х2 свободны и имеют распределения хи – квадрат с числом степеней свободы k1 и k2 соответственно. Наряду с этим пара (k1, k2) – пара «чисел степеней свободы» распределения Фишера, в частности, k1 – число степеней свободы числителя, а k2– число степеней свободы знаменателя. Распределение случайной величины F названо в честь великого британского статистика Р.Фишера (1890-1962), деятельно применявшего его в собственных работах.

Распределение Фишера применяют при проверке догадок об адекватности модели в регрессионном анализе, о равенстве дисперсий и в других задачах прикладной статистики [8, 9, 11, 16].

Выражения для функций распределения хи — квадрат, Стьюдента и Фишера, их характеристик и плотностей, и таблицы, нужные для их применения на практике, возможно отыскать в особой литературе (см., к примеру, [8]).