Центральная предельная теорема.функция лапласа

ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА

— одна из наиболее значимых предельных теорем возможностей теории, обрисовывающая асимптотику при громадных N распределения возможностей суммы N случайных размеров.

Наиб. легко Ц. п. т. формулируется для суммы

N первых участников нескончаемой последовательности свободных и одинаково распределённых случайных размеров

в предположении, что существуют, по крайней мере, два первых момента у каждой величины:

(и эти моменты однообразны для всех n). В соответствии с наиб. несложной предельной теореме теории возможностей — солидных чисел закону, случайная величина

с возможностью, близкой к единице, принимает значения порядка o(N )при N. Более совершенно верно это указывает, что для любого e0 возможность

при NЦ. п. т. существенно уточняет соотношение (5) при малых (если сравнивать с N) значениях VN: для любых конечных а и b возможность того, что

имеет асимптотику

либо, в противном случае говоря, возможности конечных (порядка константы) значений величины VN/.(s2 = = т22 -т21- дисперсия xn) распределены прибл. по стандартному обычному гауссовскому закону (со дисперсией 0 и средним 1). Из (4) и (6) направляться, что при солидных N сумма SN имеет форму

где x0 -стандартная обычная случайная величина. Утверждение (7) именуют в большинстве случаев Ц. п. т. в и н т е г р а л ьн о й ф о р м е.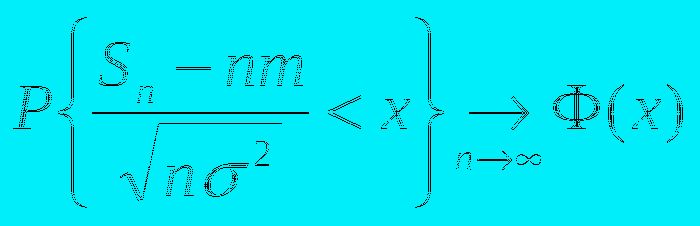 В нек-рых случаях удаётся установить не только асимптотику возможности попадания значений VN/. на конечный промежуток ( а, b), но и асимптотику самих возможностей этих значений (для случайных размеров xn с дискретным множеством значений) либо асимптотику плотности их возможностей р N (х )(для непрерывно распределённых xn):

Утверждения этого типа на данный момент узкие, чем (7)] наз. л ок а л ь н ы м и Ц. п. т. направляться выделить, что асимптотика (7) либо (9) имеет суть для конечных (порядка 1) значенийVN/. Возможности значений VN/. порядка, растущего с N, a как раз порядка Na. для a0, описываются асимптотикой (7) весьма грубо и нуждаются в более узком оценивании. Соответствующие предельные теоремы в теории возможностей наз. теоремами о громадных отклонениях.

Условия (3) весьма значительны. Предельная асимптотика для сумм вида (1), где xn не имеют второго (и первого) момента, задаётся совсем вторыми (хорошими от обычного распределения) законами, т. н. устойчивыми распределениями.

Укажем более неспециализированные обстановки, для к-рых остаётся верной Ц. п. т. (7) (либо 9):

— при, в то время, когда величины x1, x2, …, xn,… распределены не одинаково, и при условии, что у этих размеров существуют оба первых момента (3), и при дополнит. условии нек-рой равномерности (условие Линдеберга, см. [1]);

— в случае если требование независимости размеров xi, i=1, 2, … нарушено, но сохраняется в определ. смысле не сильный зависимость на большом растоянии отстоящих друг от друга размеров xi и xj, в то время, когда |i-j| — громадно (более совершенно верно см. [2]);

— возможно разглядывать не только последовательности случайных размеров, но и более неспециализированные их совокупности, скажем, случайные поля {xt, tZv на v -мерной решётке. Пускай выполнены условия (3) и величины xt и xs, t, sZv, при громадных |t — s|слабо зависимы. Тогда для любого большого и регулярного конечного множества LZvсуммы

асимптотически имеют вид:

st2 — дисперсия xt (см. [3]);

— не считая сумм размеров из одной и той же нескончаемой последовательности (2) возможно разглядывать т. н. схему серий, т. е. нескончаемую совокупность конечных последовательностей:

растущей длины, ns, s. Тогда для суммы

при определ. условиях кроме этого верна Ц. п. т.

Функция Лапласа

Отыщем возможность попадания случайной величины, распределенной по обычному закону, в заданный промежуток.

Обозначим

Тогда

Т.к. интеграл не выражается через элементарные функции, то вводится в рассмотрение функция

которая именуется функцией Лапласаили интегралом возможностей.

Значения данной функции при разных значениях х посчитаны и приводятся в особых таблицах.

Ниже продемонстрирован график функции Лапласа.

Функция Лапласа владеет следующими особенностями:

1) Ф(0) = 0;